공유메모장
DFS로 그래프 탐색 예제(1) - s-t패스 구하기, 이분 그래프 판정 본문
DFS에 대한 내용은 이곳을 참고해주세요.
깊이 우선 탐색(DFS) 유향 그래프 -JAVA 구현
유향 그래프와 무향 그래프의 차이점 그래프에서 유향 그래프와 무향 그래프의 차이는 변(간선)을 이루는 꼭짓점(노드)들이 서로서로 연결되어있는지, 아니면 편도로 연결되어 있는지이다. 유
nologic-07.tistory.com
1. s-t패스 구하기
시작점인 s부터 도착점 t까지 갈 수 있는 길이 존재하는지 확인하도록 한다.
위 링크의 예제를 조금만 변형하면 금방 로직을 구현할 수 있다.
위 링크의 예제에서는 모든 꼭짓점을 순환하기 위해 main에서도 for문을 사용하였다.
s-t패스 문제는 출발점인 s에 대해서만 dfs를 수행하면 되기 때문에 main에 for문을 사용하지 않는다.
s를 출발점으로 dfs를 수행해서 seen배열에 도착점인 t 인덱스가 true인지 false인지 확인하면 패스의 존재 유무를 알 수 있다.
전체코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
public class Main {
static boolean[] seen; //방문 여부 배열
static int[][] G; //유향 그래프 배열
static int N,M;
static void dfs(int[][] G, int v){
seen[v] = true;
// System.out.print(v+ " ->");
for(int next_v : G[v]){
if(next_v == -1) continue; //두 꼭짓점이 관계성을 가지지 않을 때는 continue
if(seen[next_v] ) continue; //이미 방문한 적 있는 꼭짓점이라면 continue
dfs(G, next_v); //재귀호출
}
}
public static void main(String[] args) throws IOException {
BufferedReader bf= new BufferedReader(new InputStreamReader(System.in));
String input[]=bf.readLine().split(" ");
N = Integer.parseInt(input[0]); //꼭짓점의 개수 N
M = Integer.parseInt(input[1]); //변의 개수 M
G = new int[N][N];
seen= new boolean[N];
for(int n=0; n<N; n++){
Arrays.fill(G[n],-1); //두 꼭짓점 사이에 연결이 없는 경우는 -1
}
Arrays.fill(seen,false); //seen 배열의 초깃값은 false
for(int i=0; i<M; i++){
input = bf.readLine().split(" ");
int a = Integer.parseInt(input[0]);
int b= Integer.parseInt(input[1]);
G[a][b] = b; // a->b 일 때 G[a][b] = b 값을 저장한다.
}
//input process
//====추가된 코드====
int s= 1;
int t= 7;
dfs(G,s);
if(seen[t]){
System.out.println( s+"->"+t +": true");
}
//========
//main process
}
}
2. 이분 그래프 판정
이분그래프란 그래프의 노드를 이분하는데, 같은 집합의 노드들은 서로서로 변(연결)이 없는 것이다.
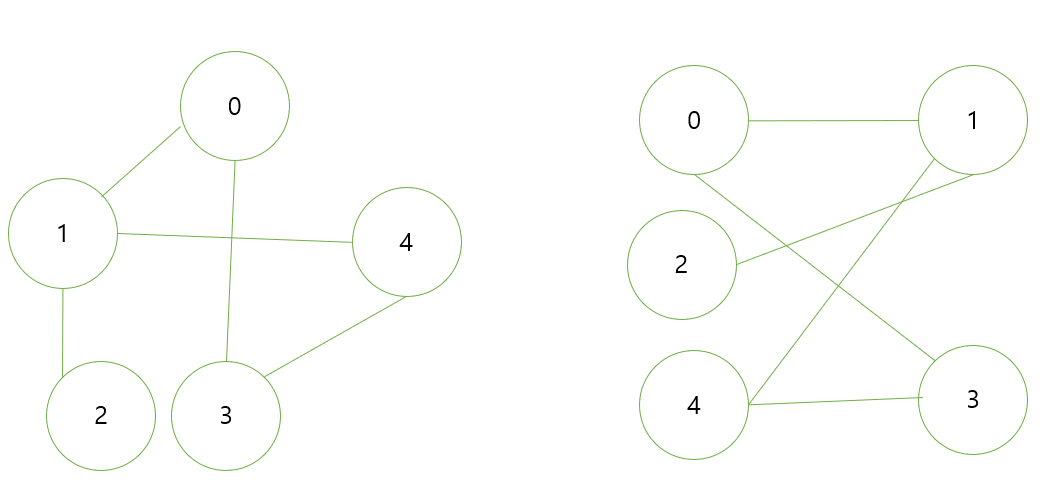
이분 그래프를 판정하기 위한 로직은 아래와 같다
1. G에서 v를 뽑아 흰색으로 칠한다. 그렇다면 v와 인접하는 노드는 모두 검정색이어야 한다. (인접하는 노드, 즉 연결되는 노드는 같은 집합에 속할 수 없기 때문이다.)
2. 흰색 노드와 인접하면 모두 검정으로 칠하고, 검정 노드와 인접하면 모두 흰색으로 칠한다.
3. 이 과정에서 양 노드가 같은 색인 경우를 발견한다면 이분 그래프가 아니다.
4. 색이 이미 정해진 경우라면 탐색하지 않는다.
(색이 정해진 노드에 대해 아직 색이 정해지지 않은 노드가 연결되어 있어도 main에서 for문 돌면서 방문하지 않은 모든 노드를 최소 1번씩 확인할 것이다.)
전체코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
public class Main {
static int[] seen; //방문 여부 배열
static int[][] G; //유향 그래프 배열
static int N,M;
static boolean dfs(int[][] G, int v, int cur){
seen[v] = cur;
System.out.print(v+ " ->");
for(int next_v : G[v]){
if(next_v == -1) continue; //두 꼭짓점이 관계성을 가지지 않을 때는 continue
//인접한 꼭짓점 색이 이미 정해져있는 경우
if(seen[next_v]!= -1){
//같은 색이 인접하면 이분 그래프가 아님
if(seen[next_v]==cur) {
System.out.println(v+" " +next_v);
return false;
}
//색이 정해져 있으면 탐색하지 않음
continue;
}
//인접 꼭짓점 색을 바꾸고 재귀적으로 탐색
//false가 반환되면 false를 돌려줌
if(!dfs(G, next_v, 1-cur)){
System.out.println(v+" "+next_v);
return false; //재귀호출
}
}
return true;
}
public static void main(String[] args) throws IOException {
BufferedReader bf= new BufferedReader(new InputStreamReader(System.in));
String input[]=bf.readLine().split(" ");
N = Integer.parseInt(input[0]); //꼭짓점의 개수 N
M = Integer.parseInt(input[1]); //변의 개수 M
G = new int[N][N];
seen= new int[M];
for(int n=0; n<N; n++){
Arrays.fill(G[n],-1); //두 꼭짓점 사이에 연결이 없는 경우는 -1
}
Arrays.fill(seen,-1); //seen 배열의 초깃값은 false
for(int i=0; i<M; i++){
input = bf.readLine().split(" ");
int a = Integer.parseInt(input[0]);
int b= Integer.parseInt(input[1]);
G[a][b] = b;
G[b][a] = a; // 해당 로직은 무향 그래프를 전제로 하기 때문에 변을 이루는 꼭짓점을 서로서로 이어준다.
}
//input process
boolean is_bipartite = true; //이분그래프 flag
for(int v=0; v<N; v++){
if(seen[v]!=-1) continue; //방문한 적 있는 꼭짓점은 continue
if(!dfs(G,v,0)){ is_bipartite = false;
}
}
System.out.println(is_bipartite);
//main process
}
}
teseCase
5 5
1 0
1 2
0 3
3 4
1 4
'알고리즘' 카테고리의 다른 글
| Union Find(유니온파인드), 서로소 집합을 활용한 사이클 판별 (0) | 2023.09.13 |
|---|---|
| 데이크스트라, 다익스트라 (dijkstra) 알고리즘 (0) | 2023.09.12 |
| 깊이 우선 탐색(DFS) 유향 그래프 -JAVA 구현 (0) | 2023.08.16 |
| Union-Find 개선법 : union by size, 경로 압축 (0) | 2023.08.11 |
| Union Find(유니온 파인드) - 연관 문제: 백준(1717번) 집합의 표현 (0) | 2023.08.11 |



